[C++] How can we save time to flatten the Complex Terrain in 'MINECRAFT' (BackJoon_18111)

INTRODUCTION

 

The Website ' BACKJOON ' has lots of interesting algorithm problems.

 

Although I'm not a software engineer for website or algorithm, but solving algorithm problems makes me deeply think about how to go step by step and optimize. It's similar with mathematics or physics.

 

But, be careful !

This post contains code many people said that this kinds of approach is wrong. (But I never think so), so please just take a look.

 

If you have played 'MINECRAFT', it may help to understand the conditions of the problem.

 

 

 

**** Problem number 18111, BACKJOON (https://www.acmicpc.net/problem/18111)

 

CONDITION

 

Suppose you're playing the ' MINECRAFT ', the world full of 1 X 1 X 1 blocks. It is a 3-Dimensional world that freely dig or build a house. Even If you have enough resources to build a house, uneven terrain is not appropriate, so you should ' flatten ' the given Area.

 

 

You can do 2 kinds of Action : 

 

1. Eliminate one Block on the top of (i, j) Coordinate and put it in the Inventory.

2. Take out one Block in the Inventory and lay it on the top of (i, j) Coordinate.

 

 

First Action takes 2 seconds and Second Action takes 1 second. In ' MINECRAFT ', there's a concept of Time, so If the Sun goes down, scary monsters will come out. Therefore you should finish flatting quickly.

 

 

Print the minimum time taken for the ' flatting ' and Height of the Ground in that case

 

There are no empty spaces (such as cave) under the Given Area and you can't bring Blocks from outside. Also, height of the Land can't exceed 256 Blocks and be negative.

 

 

INPUT

 

1. N, M, B is given in the First Line. (1 ≤ M, N ≤ 500, 0 ≤ B ≤ 6.4 × 107)

2. Height of the Land is given by each M number of Integers of the N number of Rows in the Second Line.

If you find multiple answers, print the highest one.

 

EXAMPLE

 

In this Example, 3X4 Terrain has given and we have 99 Blocks in the Inventory. We easily assume that if we dig (3,4) Block, the Terrain will be flatten.

 

Consequently, 'Dig' takes 2 seconds and the Terrain is flatten with 0-Height, so the answer is {2, 0}. 

 

 

MY LOGIC

 

To be honest, I chose this problem because I familiar with the game ' MINECRAFT ' and it wasn't look that hard,,,Before 9 time of attempts,,, Then I realized something was wrong.

 

 

But ! Let's Go !

 

 

Let's assume we have the following Input :

3 4 5

64 64 64 64

64 64 64 64

64 64 64 62

 

 

First, As mentioned, There should be no empty spaces under the Given Terrain. So if we divide the Given Terrain by one height Layers, 65 Layers is created (Height : 64 ~ 0) and each top 2 Layers (64, 63) has Hole in (3,4) coordinate.

 

For a Layer which has one Hole in Whole Matrix, If we cover one Hole, the Worked Time is 1 Second. But if we dig other 11 Blocks, the Worked Time is 11*2, 22 Seconds.

 

 

So In the case of one Layer, How can we determine ' Dig ' or ' Cover ' ?

 

According to time of Work, Dig is 2 and Cover is 1. So in 3X4 Layer, if this Layer has N number of Holes, there're (12-N) number of Blocks are left.

Therefore, If we cover the Holes, the Worked Time is N seconds. But If we cover, then the Worked Time is 2*(12-N).

 

Then the number N which makes these two equation equal is the Criterion for Determine. 

If the number of Holes exceeds the Criterion, Digging the protruding Blocks is a better option to save time.

If not, Covering Holes with the Blocks in the Inventory is a better option.

 

In a 3X4 Matrix case, Criterion is N = 2*(12-N), N = 8.

 

 

More general, we find out the Criterion is (MXN)*(2/3) in a MXN Matrix.

For the circumstance that both M and N are not divisible by 3, Criterion should be initialized with 'float' not 'int'.

 

 

But What if we don't have enough Blocks to cover the Holes in the Inventory ?

 

This should be considered in the first process. No only defined in the first Layer, If we find out ' Cover ' is a better option for the Top Layer, then we should cover Whole Layers top to bottom because empty spaces is not allowed.

 

Check example below.

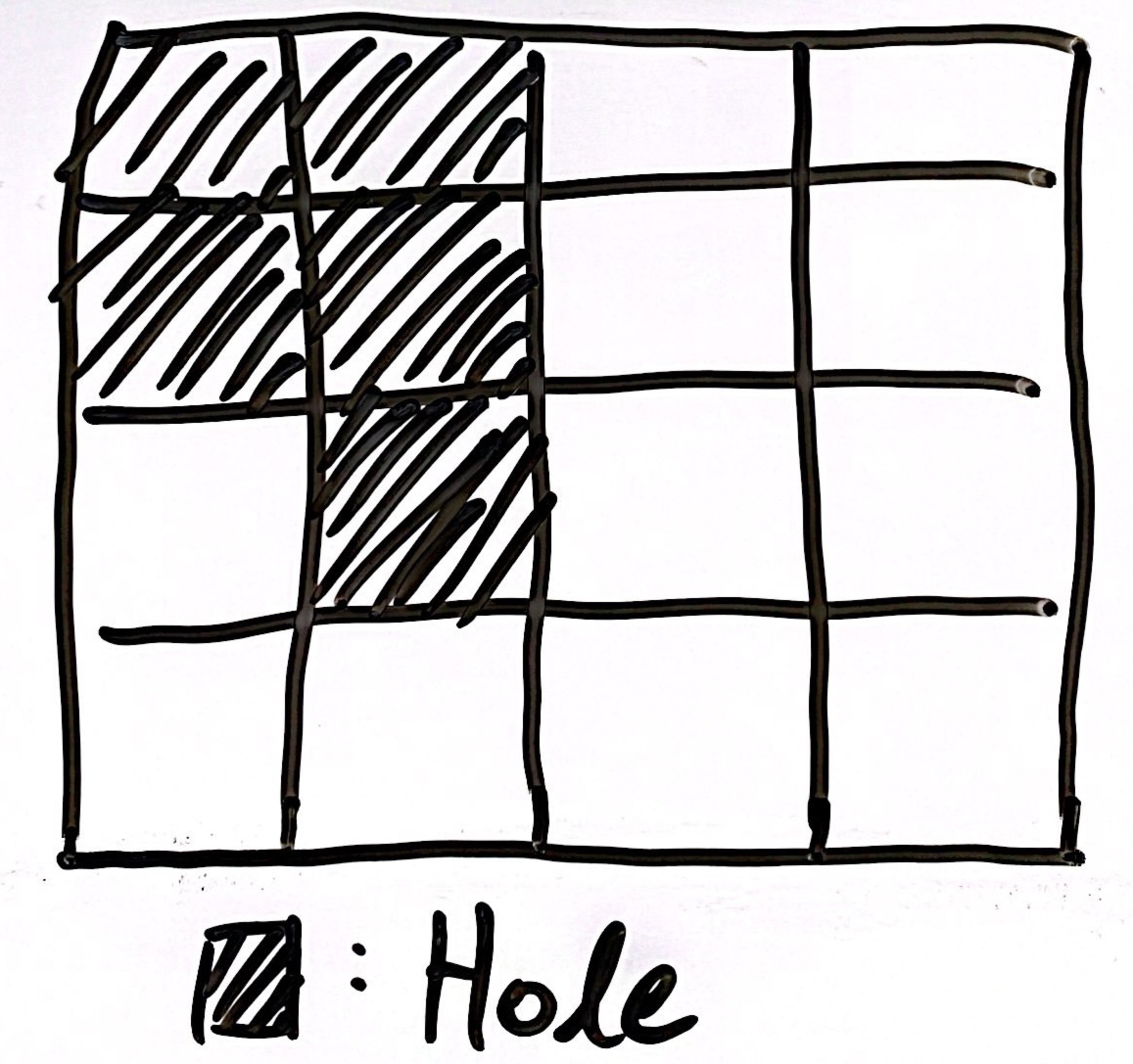
Suppose this is a cross section of some Terrain and its Top Layer has 4 Blocks and 2 Holes. If we cover them, it takes 2 seconds and if we dig, it takes 4 seconds. In this case, cover is obviously a better option.

 

However, what If we have less than 5 Blocks ? If we have 2 Blocks, the 2 Holes in the Top Layer will be covered but we can't cover other Blocks below.

 

Consequently, even if ' Cover ' is a determined for one specific Layer, if we don't have enough Blocks to cover all the Layers below, ' Dig ' is evitable option. 

 

 

So At first, the number of Holes of Whole Layers should be figured out and after processing one Layer, re-calculates the number of Holes of remaining Layers and compare with the number of Blocks in the Inventory.

 

 

Don't forget that when we dig Blocks, the number of Blocks in our Inventory increase as many as (Area - Holes) !

 

Check Code below.

 

CODE

#include <iostream>
#include <vector>
#include <iterator>
#include <algorithm>
#include <numeric>
#include <map>
using namespace std;

class Terrain {
public :
    Terrain() = default; // Default Constructor
    Terrain(std::vector <vector <int>> _Terrain, size_t _Row_Size, size_t _Col_Size) // Constructor
            : Components(_Terrain),Row_Size(_Row_Size), Col_Size(_Col_Size){};
    Terrain(int Value, size_t _Row_Size, size_t _Col_Size) : Row_Size(_Row_Size), Col_Size(_Col_Size){
        std::vector <std::vector<int>> Valued_Vec;
        for(int i=0; i<_Row_Size; i++){
            std::vector<int> temp;
            for(int j=0; j<_Col_Size; j++)
                temp.push_back(Value);
            Valued_Vec.push_back(temp);
        }
        Components = Valued_Vec;
    }

    Terrain (const Terrain& _Terrain) : Components(_Terrain.Components),Row_Size(_Terrain.Row_Size), Col_Size(_Terrain.Col_Size) {} // Copy Constructor
    Terrain (const Terrain&& _Terrain) : Row_Size(std::move(_Terrain.Row_Size)), Col_Size(std::move(_Terrain.Col_Size)){
        Components = std::move(_Terrain.Components);} // Move Constructor
    ~Terrain() noexcept = default; // Destructor
    int& operator[] (std::pair<int ,int> _Where){ // Index Operator

        int index_Row = _Where.first;

        int index_Col = _Where.second;

        return Components[index_Row][index_Col];

    }
    friend int MAX(Terrain _Terrain); // Top Layer Determinant
    friend int MIN(Terrain _Terrain, int Max); // Bottom Layer Determinant
    friend pair<int,int> Deter(Terrain _Terrain, int B); // (Worked Time, Top Layer Position)
    friend std::ostream& operator << (std::ostream& os, const Terrain& _Terrain);

private:
    std::vector <std::vector <int>> Components {0}; // Data of Terrain
    size_t Row_Size = 0;
    size_t Col_Size = 0;
};


std::ostream& operator << (std::ostream& os, const Terrain& _Terrain){

    for(auto it = _Terrain.Components.begin(); it != _Terrain.Components.end(); it++){

        std::copy(it->begin(),it->end(),std::ostream_iterator<int>(std::cout," "));
        std::cout << std::endl;

    }

    return os;
}


std::vector <std::vector <int>> Input (int M, int N){

    std::vector <std::vector <int>> Terrain;

    for(int i=0; i<M; i++){

        std::vector <int> Vec_Temp;

        for(int j=0; j<N; j++){

            int Temp;

            cin >> Temp;

            Vec_Temp.push_back(Temp);
        }

        Terrain.push_back(Vec_Temp);
    }

    return Terrain;
}


int MAX (Terrain _Terrain) {

    int Max = 0;

    for(auto it : _Terrain.Components){

        int Max_Temp = *std::max_element(it.begin(),it.end());

        if(Max_Temp > Max)
            Max = Max_Temp;
    }

    return Max;
}


int MIN(Terrain _Terrain, int Max){

    int Min = Max;

    for(auto it : _Terrain.Components){

        int Min_Temp = *std::min_element(it.begin(),it.end());

        if(Min_Temp < Min)
            Min = Min_Temp;
    }

    return Min;
}


pair<int,int> Deter (Terrain _Terrain, int B){

    int Max = MAX(_Terrain);

    int Min = MIN(_Terrain, Max);

    std::vector <std::pair <Terrain,int>> Layer_info; // Top -> Bottom Layers info (0 ~ Max-Min)

    for(int i= Max; i>Min; i--){

        Terrain Terrain_Temp (0, _Terrain.Row_Size, _Terrain.Col_Size);

        int Hole_Current_Layer = 0;

        for(int j=0; j<_Terrain.Row_Size; j++){

            for(int k=0; k<_Terrain.Col_Size; k++){

                auto pa = make_pair(j,k);

                if(i > _Terrain[pa]) {
                    Terrain_Temp[pa] = 1;
                    Hole_Current_Layer++;
                }
            }

        }

        auto Pair_Temp = make_pair(Terrain_Temp, Hole_Current_Layer);

        Layer_info.push_back(Pair_Temp);
    }

    int Whole_Hole = 0;

    for(auto it : Layer_info)
        Whole_Hole += it.second;

    std::cout << "The number of Holes in Whole Layers is : " << Whole_Hole << std::endl;



    pair <int, int> Result = {0,0};

    int Time = 0;
    int Level = Max;


    int Area = _Terrain.Row_Size*_Terrain.Col_Size;

    float Criterion = Area *2 / 3;




    int Hole_Left = Whole_Hole;

    for(int i=0; i<Max-Min; i++){

        if(B >= Hole_Left){ // There are enough Blocks to cover below Layers, so we have options, cover or cut

            if(Layer_info[i].second <= Criterion){ // Cover is a better option to save time
                Time += Layer_info[i].second; // Filling takes 1-sec
                B -= Layer_info[i].second; // The Inventory(B) is consumed equal to the number of Holes
            } else { // Cutting is a better option to save time
                Time += 2*(Area - Layer_info[i].second); // Cutting takes 2-sec
                Level--; // Top Layer is cut off
                B += (Area - Layer_info[i].second); // The Inventory(B) is filled equal with the number of Area - Holes
            }

        }

        else { // There aren't enough Blocks to cover below Layers, so we only have to cut top layers

            Time += 2*(Area - Layer_info[i].second); // Cutting takes 2-sec
            Level--; // Top Layer is cut off
            B += (Area - Layer_info[i].second); // The Inventory(B) is filled equal with the number of Area - Holes

        }

        Hole_Left -= Layer_info[i].second; // Eliminate Top Layer's Hole

    }


    Result.first = Time;
    Result.second = Level;

    return Result;
}



int main() {

    int M = 0, N = 0, B = 0;

    std::cin >> M >> N >> B;

    vector <vector <int>> input = Input(M,N);

    Terrain Terrain(input,M,N);

    pair<int, int> Result = Deter(Terrain, B);

    std::cout << "Worked Time is : " << Result.first <<" And the height of the Terrain is : " << Result.second << std::endl;

}

 

As you noticed, Define the Terrain 'Class' is not necessary for this problem, but I was impressed by expandability of Object Oriented Language, called ' Polymorphism ', so I tried.

 

 

MY RESULT

 

And the result is not that Bad.

 

 

Another result :

 

Friend of mine shared his answer, although it was solved by python, it is unbelievably short.

He said construct algorithm which has no exception and find the value for all situations. Good Advice.

 

 

I have failed while trying to prepare for every possible situation. Actually, I also doubted myself for awhile, but after 12 times of trying, I finally passed !

I proved that I'm not Wrong ! 

 

 

WHAT I HAD LEARNED

 

In near past, when I studied C++ at school, Professor asked whole students in the class that "Are you want to be a programmer in 1998 or Modern ?". I understood what he talked, however I think 98 is not that bad option. Actually I want it.

 

A lot of tools are made and somepeople tell C and C++ is old-fashion. But I prefer Wallet to Electro-Wallet, Wrist Watch to Smart-Watch. It might quite far from professor's intention, but I prefer intuitive way to short-cut.

 

That's why I likes mathematics and Physics.

 

If you have the power to push your conviction to the end, please keep it even if it is different from others.

 

I'll keep challenging to another interesting problems and I hope I keep standing with this conviction for the rest of my  life.

 

 

Thanks for your reading and I hope you got what you wanted !

 

Reference